优化机器人动作的CMA-ES算法 python版本的api分析

Robocup3D

字数统计: 1.7k阅读时长: 8 min

 2019/07/13

首先，我先声明，本人并不研究机器学习或人工智能，这篇文章主要是为了偶尔使用一下某个算法所作的分析

1.从官网说起

首先，可以从搜索引擎很轻易搜索到它的pypi网址：
https://pypi.org/project/cma/
打开后，我们可以看到如何去安装cma。目前版本为
upload successful
这里我就把如何安装跳过，直接进入api分析：

2.API分析

这是官网用例的第一个，是在python Shell中运行的

>>> import cma
>>> help(cma)
    <output omitted>
>>> es = cma.CMAEvolutionStrategy(8 * [0], 0.5)
(5_w,10)-aCMA-ES (mu_w=3.2,w_1=45%) in dimension 8 (seed=468976, Tue May  6 19:14:06 2014)
>>> help(es)  # the same as help(cma.CMAEvolutionStrategy)
    <output omitted>
>>> es.optimize(cma.ff.rosen)
Iterat #Fevals   function value    axis ratio  sigma  minstd maxstd min:sec
    1      10 1.042661803766204e+02 1.0e+00 4.50e-01  4e-01  5e-01 0:0.0
    2      20 7.322331708590002e+01 1.2e+00 3.89e-01  4e-01  4e-01 0:0.0
    3      30 6.048150359372417e+01 1.2e+00 3.47e-01  3e-01  3e-01 0:0.0
  100    1000 3.165939452385367e+00 1.1e+01 7.08e-02  2e-02  7e-02 0:0.2
  200    2000 4.157333035296804e-01 1.9e+01 8.10e-02  9e-03  5e-02 0:0.4
  300    3000 2.413696640005903e-04 4.3e+01 9.57e-03  3e-04  7e-03 0:0.5
  400    4000 1.271582136805314e-11 7.6e+01 9.70e-06  8e-08  3e-06 0:0.7
  439    4390 1.062554035878040e-14 9.4e+01 5.31e-07  3e-09  8e-08 0:0.8
>>> es.result_pretty()  # pretty print result
termination on tolfun=1e-11
final/bestever f-value = 3.729752e-15 3.729752e-15
mean solution: [ 1.          1.          1.          1.          0.99999999  0.99999998
  0.99999995  0.99999991]
std deviation: [  2.84303359e-09   2.74700402e-09   3.28154576e-09   5.92961588e-09
   1.07700123e-08   2.12590385e-08   4.09374304e-08   8.16649754e-08]

这是优化八维Rosenbrock function的范例，初始解全部为零，初始sigma=0.5

数学最优化中，Rosenbrock函数是一个用来测试最优化算法性能的非凸函数，由Howard Harry Rosenbrock在1960年提出 [1] 。也称为Rosenbrock山谷或Rosenbrock香蕉函数，也简称为香蕉函数。
Rosenbrock函数的定义如下：
Rsenbrock函数的每个等高线大致呈抛物线形，其全域最小值也位在抛物线形的山谷中（香蕉型山谷）。很容易找到这个山谷，但由于山谷内的值变化不大，要找到全域的最小值相当困难。其全域最小值位于 (x,y)=(1,1)点，数值为f(x,y)=0。有时第二项的系数不同，但不会影响全域最小值的位置。

有了上述定义，我们仔细分析一下
es = cma.CMAEvolutionStrategy(8 * [0], 0.5)
这一句是定义了初始参数，或者叫种子值，传入一个链表和其他参数
es.optimize(cma.ff.rosen)
这一句调用了es实例中的optimize函数，传入了一个函数作为参数，这个函数就是Rsenbrock函数
es.result_pretty()
这一句就是将结果打印出来。

随后我在自己电脑上测试一下
迭代次数：

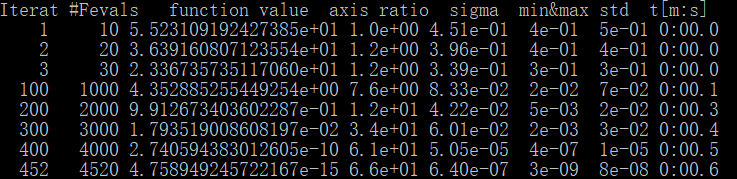
upload successful
结果

incumbent solution: [0.9999999981487978, 0.9999999982509171, 1.0000000001933775, 1.000000001462353, 1.0000000031948872, 1.0000000061217036, 1.000000011285589, 1.0000000240833469]

结果和dome差距不大。
接下来我们看官网第二个范例：

>>> import cma
>>> xopt, es = cma.fmin2(cma.ff.rosen, 8 * [0], 0.5)
    <output omitted>

这里代码简单不少，只需要将相应的参数带入即可，自己实验结果如下：

incumbent solution: [1.0000000018995456, 1.0000000018093442, 0.9999999987364477, 0.9999999987109501, 0.9999999974763141, 0.9999999978845102, 0.999999998874965, 0.9999999974149408]

和前面的方法结果差不多，在控制台打印的东西也差不多，但语法简单不少
在官网还有让结果展示更规范的dome：

>>> import cma
>>> es = cma.CMAEvolutionStrategy(12 * [0], 0.5)
>>> while not es.stop():
...     solutions = es.ask()
...     es.tell(solutions, [cma.ff.rosen(x) for x in solutions])
...     es.logger.add()  # write data to disc to be plotted
...     es.disp()
    <output omitted>
>>> es.result_pretty()
    <output omitted>
>>> cma.plot()  # shortcut for es.logger.plot()

接下来我们再在自己测试一下

>>> import cma
>>> es = cma.CMAEvolutionStrategy(12 * [0], 0.5)
(5_w,11)-aCMA-ES (mu_w=3.4,w_1=42%) in dimension 12 (seed=879114, Wed Dec 26 15:33:59 2018)
>>> while not es.stop():
...     solutions = es.ask()
...     es.tell(solutions, [cma.ff.rosen(x) for x in solutions])
...     es.logger.add()  # write data to disc to be plotted
...     es.disp()
...
could not open file outcmaesfit.dat
could not open/write file outcmaesaxlen.dat
could not open file outcmaesaxlencorr.dat
could not open file outcmaesstddev.dat
could not open/write file outcmaesxmean.dat
could not open/write file outcmaesxrecentbest.dat
WARNING ():  ('could not open/write file outcmaesfit.dat: ', (<class 'PermissionError'>, PermissionError(13, 'Permission denied'), <traceback object at 0x0000029961910B08>))
Iterat #Fevals   function value  axis ratio  sigma  min&max std  t[m:s]
    1     11 2.199434967334791e+02 1.0e+00 4.62e-01  5e-01  5e-01 0:00.0
<cma.evolution_strategy.CMAEvolutionStrategy object at 0x000002995A9D9588>
    2     22 1.483192009953597e+02 1.1e+00 4.29e-01  4e-01  4e-01 0:00.0
<cma.evolution_strategy.CMAEvolutionStrategy object at 0x000002995A9D9588>
    3     33 1.500251145830725e+02 1.2e+00 3.92e-01  4e-01  4e-01 0:00.0
    <output omitted>
   100   1100 9.363570704737704e+00 5.8e+00 1.60e-02  7e-03  3e-02 0:00.2
    <output omitted>
    <cma.evolution_strategy.CMAEvolutionStrategy object at 0x000002995A9D9588>
    <cma.evolution_strategy.CMAEvolutionStrategy object at 0x000002995A9D9588>
    <cma.evolution_strategy.CMAEvolutionStrategy object at 0x000002995A9D9588>
    <cma.evolution_strategy.CMAEvolutionStrategy object at 0x000002995A9D9588>
    <cma.evolution_strategy.CMAEvolutionStrategy object at 0x000002995A9D9588>
    <cma.evolution_strategy.CMAEvolutionStrategy object at 0x000002995A9D9588>
    <cma.evolution_strategy.CMAEvolutionStrategy object at 0x000002995A9D9588>
    <cma.evolution_strategy.CMAEvolutionStrategy object at 0x000002995A9D9588>
   681   7491 8.477781332691924e-15 7.6e+01 6.85e-08  2e-09  5e-08 0:01.4
    <cma.evolution_strategy.CMAEvolutionStrategy object at 0x000002995A9D9588>

>>> es.result_pretty()
termination on tolfun=1e-11
final/bestever f-value = 8.477781e-15 8.477781e-15
incumbent solution: [1. 1. 1. 1. 1. 1. 1. 1. ...]
std deviations: [1.64793484e-09 1.62131324e-09 1.56866080e-09 1.63444023e-09
 1.75755218e-09 1.95473201e-09 2.58734723e-09 4.15379464e-09 ...]
CMAEvolutionStrategyResult(xbest=array([1.        , 1.        , 1.        , 1.        , 1.        ,
       1.        , 1.        , 1.        , 1.        , 1.00000001,
       1.00000001, 1.00000002]), fbest=8.477781332691924e-15, evals_best=7481, evaluations=7491, iterations=681, xfavorite=array([1.        , 1.        , 1.        , 1.        , 1.        ,
       1.        , 1.        , 1.        , 1.        , 1.        ,
       1.00000001, 1.00000001]), stds=array([1.64793484e-09, 1.62131324e-09, 1.56866080e-09, 1.63444023e-09,
       1.75755218e-09, 1.95473201e-09, 2.58734723e-09, 4.15379464e-09,
       7.18357672e-09, 1.37685816e-08, 2.72303150e-08, 5.43614293e-08]))

可以看到，这个迭代输出就更规范了
而且也可以输出到文件里
这是因为cma算法完成后应该会调用es.stop()
在官网上还有一些更细节的logger options 这里就不赘述

>>> import cma
>>> cma.s.pprint(cma.CMAOptions('erb'))
{'verb_log': '1  #v verbosity: write data to files every verb_log iteration, writing can be time critical on fast to evaluate functions'
 'verbose': '1  #v verbosity e.v. of initial/final message, -1 is very quiet, not yet implemented'
 'verb_plot': '0  #v in fmin(): plot() is called every verb_plot iteration'
 'verb_disp': '100  #v verbosity: display console output every verb_disp iteration'
 'verb_filenameprefix': 'outcmaes  # output filenames prefix'
 'verb_append': '0  # initial evaluation counter, if append, do not overwrite output files'
 'verb_time': 'True  #v output timings on console'}

除此之外，官网上还说，这个算法适合5到100的解空间
并且至少需要100次迭代才能得到差不多的数值
还有如果不知道选项的含义，可以用